Linear Search Algorithm in Gene Name Batch Viewer

Gene Name Batch Viewer

For given gene list, the viewer is able to quickly list all gene names which is a straight forward feature.  This manual will  mainly focus on Related Genes/Terms Search algorithms provided by this viewer as well.
The Related Gene Searching Algorithm

1.  Introduction
2.  A Hypothetical Example
3.  Options and Results
4.   Kappa Statistics
The Related Annotation Term Searching Algorithm

1.  Introduction
2.  A Hypothetical Example
3.  Options and Results
4.   Kappa Statistics

The Related Gene Searching Algorithm
    1. Introduction

Any given gene is associating with a set of annotation terms. If genes share similar set of those terms, they are most likely involved in similar biological mechanisms. The algorithm adopts kappa statistics to quantitatively measure the degree of the agreement how genes share the similar annotation terms. Kappa result ranges from 0 to 1. The higher the value of Kappa, the stronger the agreement. Kappa more than 0.7 typically indicates that agreement of two genes are strong. Kappa values greater than 0.9 are considered excellent.
    2. A Hypothetical Example


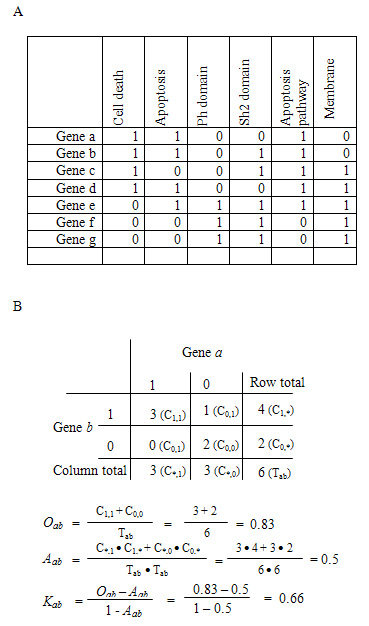Figure: A hypothetical example to detect gene-gene functional relationship by kappa statistics. A. The all-redundant and structured terms are broken into ‘independent’ terms in a flat linear collection. Each gene associates with some of the annotation term collection so that a gene-annotation matrix can be built in a binary format, where 1 represents a positive match for the particular gene-term and 0 represents the unknown. Thus, each gene has a unique profile of annotation terms represented by a combination of 1s and 0s. B. For a particular example of genes a and b, a contingency table was constructed for kappa statistics calculation. The higher kappa score (0.66) indicates that genes a and b are in considerable agreement, more so than by random chance. To flip the table 90 degrees, the kappa score of term-term can be achieved, based on the agreement of common genes (not shown).
    3. Options and Results



Overlap Threshold Option:


The minimum number of terms in common between query gene and candidate gene  for the consideration in the searching algorithm. For most cases, it should be above 3 for the statistical reasons.

Kappa Threshold Option:


The minimum Kappa value for the consideration. The higer of threshold, the stricter of the search. Default is 0.25 and setting range from 0 to 1.

Related Gene Column:


The result of related genes to the query gene.

Agreement (Kappa) Column:


The agreement score calculated by Kappa statistics. Kappa result ranges from 0 to 1. The higher the value of Kappa, the stronger the agreement. Kappa more than 0.7 typically indicates that agreement of two genes are strong. Kappa values greater than 0.9 are considered excellent

Evidence Page:

The term numbers of agreement and disagreement between query gene and hit gene. These numbers are used to calculate the agreement score (Kappa or Fisher Exact).
    4. Kappa Statistics

The Kappa Statistic is a chance corrected measure of agreement between two sets of categorized data. Kappa result ranges from 0 to 1. The higher the value of Kappa, the stronger the agreement. If Kappa = 1, then there is perfect agreement. If Kappa = 0, then there is no agreement. For further details about Kappa statistics please refer to "A coefficient for agreement of nominal scales" Educational and Psychological Measurement 20: p 37-46.
top
The Related Term Searching Algorithm
     1.  Introduction

Typically, a biological process/term is a cooperationof a set of genes. If two or more biological processes are done by similar set of genes, the processes might be related in the biological network somehow. To identify the related biological processes/terms can help biologists to assemble a bigger biological picture for better understanding biological themes. This algorithm adopts kappa statistics to quantitatively measure the degree of the agreement how terms share the similar participating genes for. After scanning all pairs of given term to other terms, the closely related terms to the given one could be listed and sorted. Kappa result ranges from 0 to 1. The higher the value of Kappa, the stronger the agreement. Kappa more than 0.7 typically indicates that agreement of two genes are strong. Kappa values greater than 0.9 are considered excellent

    2. A Hypothetical Example

After reducing participating gene information to its most basic level using a binary mode (1 represents ‘Yes’ and 0 is ‘No’), term A and B share the same participating genes 1, 3, and n, in contrast that term A and C only share gene 3. Obviously, the relationship of term A-B is stronger than that of term A- C.


Raw Data Table:


 gene 1
gene 2  
gene 3 
gene n
Term A   1
 0
 1
 1
Term B
 1
 0
 1
 1
Term C
 0
 0
 1
 0
Term D
 1
 0
 0
 1

2x2 contigency tables for both, based on above raw data:

Term A
Term B
    1
      0
   1 
3 genes
 0 gene
   0
 0 gene
 1 gene


Term A
Term C
     1
      0
   1
 1 gene
 0 gene
   0
 2 genes
 1 gene

Kappa for Term A-B = 1; Kappa for Term A-C = 0.2; Therefore, the relationship of A-B is much stronger than that of A-C.
    3. Options and Results

Overlap Threshold Option:


The minimum number of genes in common between query term and candidate term for the consideration in the searching algorithm. For most cases, it should be above 3 for the statistical reasons.

Kappa Threshold Option:

The minimum Kappa value for the consideration. The higer of threshold, the stricter of the search. Default is 0.25 and setting range is from 0 to 1.


Related Terms Column:


The result of related terms to the query term.

Similarity(Kappa) Column:


The agreement score calculated by Kappa statistics or Fisher Exact. Kappa result ranges from 0 to 1. The higher the value of Kappa, the stronger the agreement. Kappa more than 0.7 typically indicates that agreement of two terms are strong. Kappa values greater than 0.9 are considered excellent

Evidence Page:


The gene numbers of agreement and disagreement between query term and hit term. These numbers are used to calculate the agreement score (Kappa or Fisher Exact).
    4. Kappa Statistics

The Kappa Statistic is a chance corrected measure of agreement between two sets of categorized data. Kappa result ranges from 0 to 1. The higher the value of Kappa, the stronger the agreement. If Kappa = 1, then there is perfect agreement. If Kappa = 0, then there is no agreement. For further details about Kappa statistics please refer to "A coefficient for agreement of nominal scales" Educational and Psychological Measurement 20: p 37-46.

top
Last Updated:  Feb. 2005